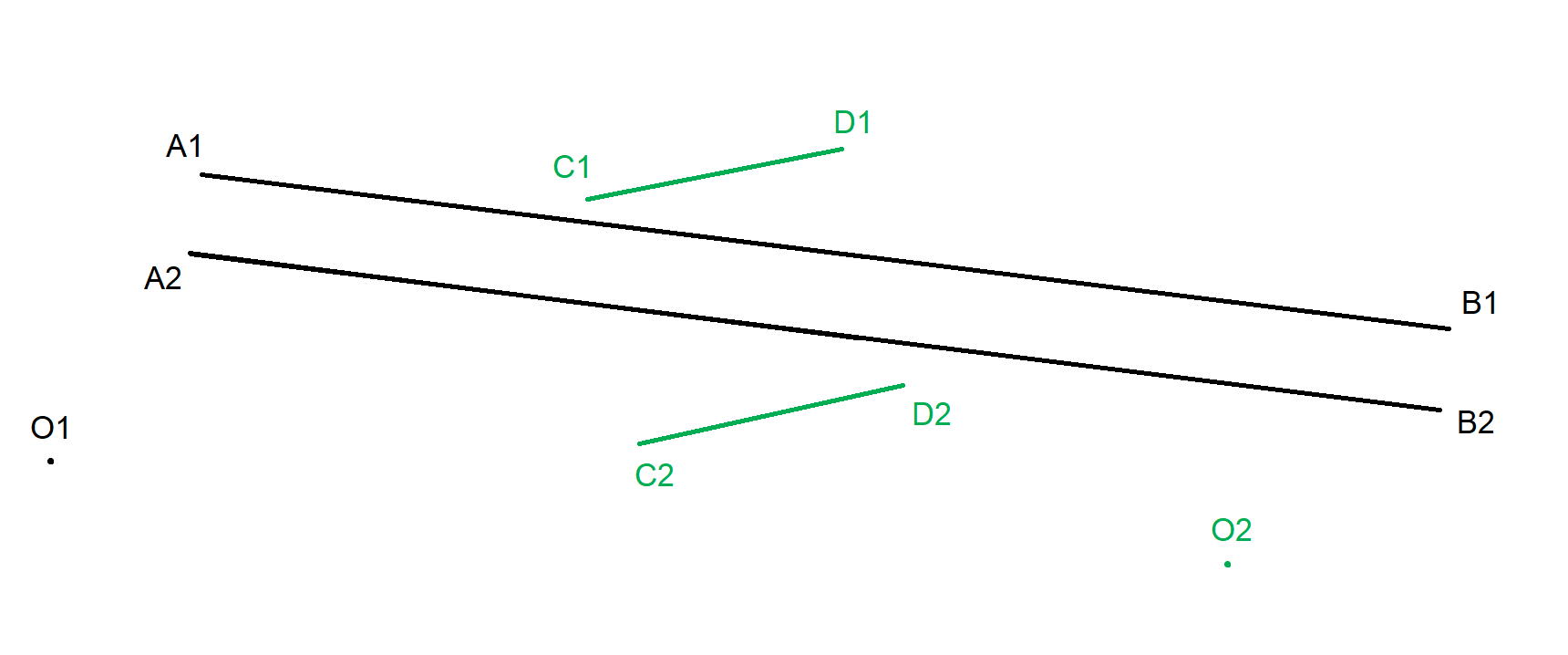
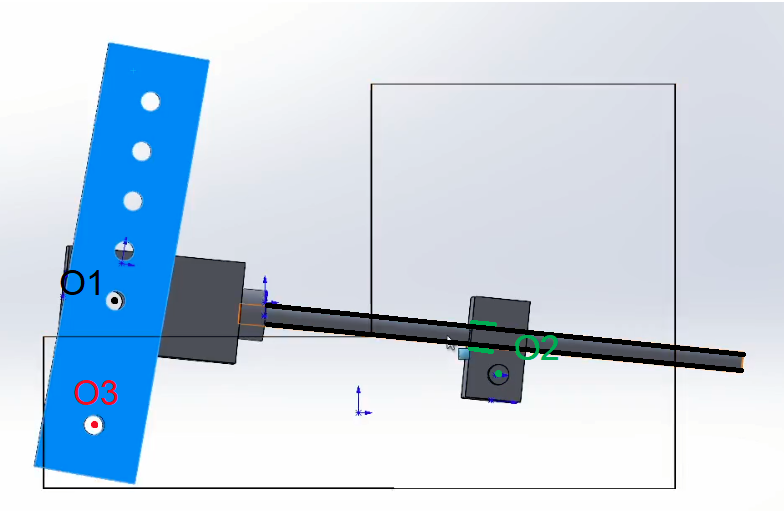
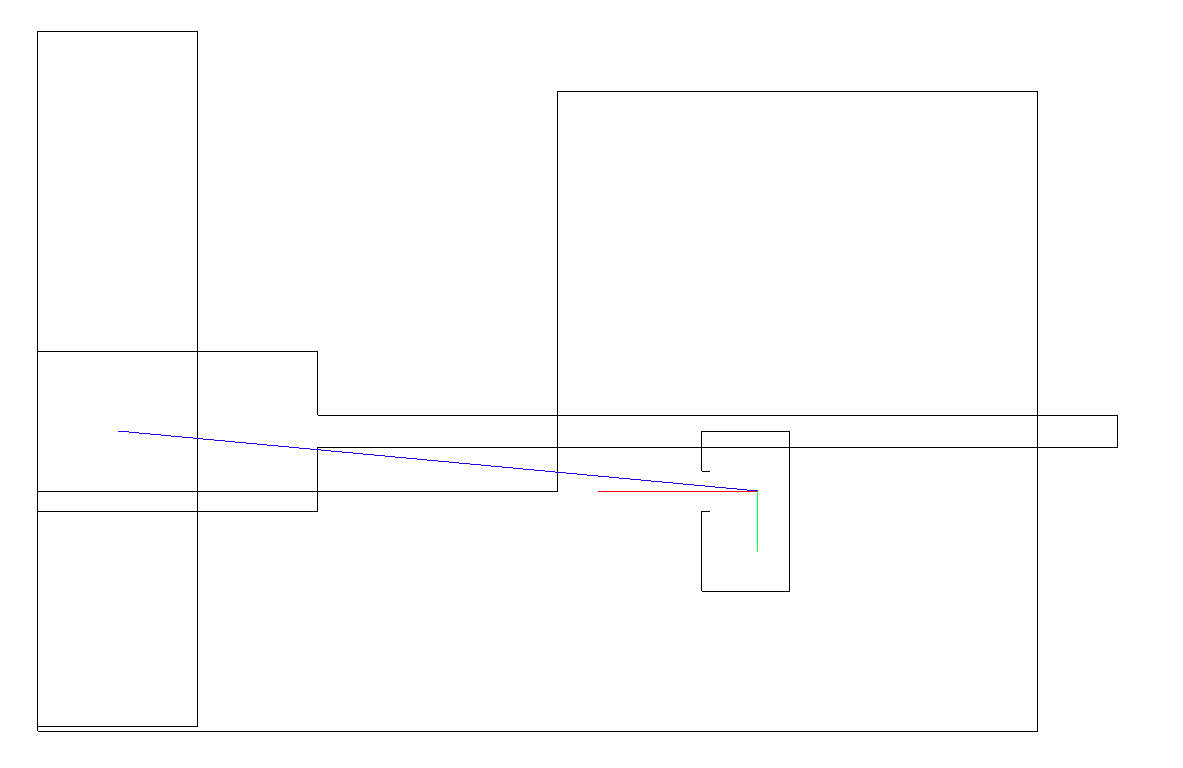
анон, помоги решить проблему. вот у меня есть 2 отрезка A1B1 и A2B2, координаты их конечных точек я
Аноним
29/05/25 Чтв 16:23:55
№
1
задача: насколько возможно оптимальным способом сразу высчитать углы поворота для A1B1 A2B2 и для C1D1 C2D2 таким образом, чтобы ни один отрезок из A1B1 A2B2 не пересекал C1D1 C2D2. т.е. чтобы черные отрезки не пересекались с зелеными, а были между ними всегда, для этого надо как-то высчитать углы поворотов для двух компонент.
чтобы было более понятно, мне надо симулировать подобный механизм (пик 2 и 3). надеюсь понятно объяснил
Ну так вращай A1B1 A2B2 как хочешь и проверяй на пересечение с C1D1 C2D2
>Ну так вращай A1B1 A2B2 как хочешь и проверяй на пересечение с C1D1 C2D2
Вращай A1B1 и проверяй на пересечение C1D1
фикс
это будет как перебор, нужно будет городить кучу костылей, чтобы при случае чего сделать откат к какому-то углу и пробовать поворачивать зеленые отрезки. это будет как угадайка. не эффективно. вот я поэтому думал может можно как-то геометрически рассчитать эти углы поворота?
посмотри внимательно на видео, там не просто вращение происходит. этот длинный шток (A1B1 и A2B2) сначала как-бы идет вниз, а затем в какой-то момент начинает правый конец поднимать вверх, меняя наклон в противоположную сторону.
еще добавлю. это поведение будет зависеть полностью от расположения осей O1 и O2. а я как раз потом и хочу менять эти оси, чтобы потом отсортировать результаты по длине хода (насколько глубоко А1B1 и A2B2 проходят внутрь отверстия, грани которого ограничиваются C1D1 и C2D2) и выбрать нужные, оптимальные для меня
>геометрически рассчитать эти углы поворота
Так ты геометрически расчитываешь пересечение при повороте, ты же знаешь как найти пересечение двух векторов в 2d? Вооот. А забить все точки пересечения это хуета.
вот смотри. я повернул на 5 градусов. получилось перечение. с этого момента я должен вращать либо вокруг O1, либо вокруг O2, либо O1 и O2 вместе, подбирая углы так, чтобы выполнилось условие НЕ пересечения. допустим я начал вращать только вокруг O1 с каким-то шагом в левую сторону (т.к. пересечение произошло в нижнем отрезке). и вот я дрочу по 0,01 градусу, чтобы не проебать момент... потом бац: СРАЗУ ПЕРЕСЕЧЕНИЕ ВВЕРХУ, А ВНИЗУ ЕГО НЕТ. начинаю так же вращать уже зеленые отрезки вокруг О2. и все по новой. я могу либо попасть снова в такую ситуацию. и придется обратно вращат ьчерные отрезки вокруг О1 снова. короче, это все сводится к какой-то хуйне, где ты ловишь углы ОБЕИХ компонент так, чтобы выполнилось условие. это дроч. это костыли. это хуйня.
>Так ты геометрически расчитываешь пересечение при повороте, ты же знаешь как найти пересечение двух векторов в 2d?
ну я определил, что где-то у меня произошло пересечение. и что это дает мне? я должен все равно подбирать эти углы, потому что я не знаю уравнения по которому можно было бы сразу рассчитать эти углы
можно поподробней? каких именно точек? всех черных и зеленых отрезков? относительно чего? своей оси вращения т.е. О1 и О2?
>pi/2 pi 3pi/2 2pi
что-то одно любое выбрать?
>это будут экстремумы координат
от куда такая уверенность? положение изначальное точек ведь может быть любым абсолютно. если я правильно вообще понял что ты подразумеваешь под экстремумами. я не совсем в общем понял твою идею.
провел зеленую линию от центра вращения до середины отверстия (перпендикулярно). от сюда горизонтально провел произвольную линию (красная). так же горизонтальную уже готовую линию (не стал новую рисовать), которая является самим штоком. и соединил центра узлов вращения двух деталей синей линией. все эти отрезки превратил в вектора, и относительно синей линии находил угол между векторами. это тот самый угол на который надо повернуть каждую деталь.
вроде похоже на то, что надо было, но заметил проблему - когда начинаю далеко вращать, синяя и красные линии начинают расходиться. в чем может быть проблема?
а все исправил. не обновлял другой конец синей линии
>>3466762
Че у вас здесь происходит?
Это че за машина ебалка?
это я хотел визуализировать расположение направляющей для штока с пружиной, чтобы оптимальное его расположение выявить для педалей игровых. там где красное - ход пружины максимален. черное - превышает. зеленое - минимальный. но у меня еще не дописано и тут ошибки есть и опущенные нюансы. позже исправлю
короче доделал. теперь норм все. на графике угол педали A(o) и сила пружины F(kg) при угле
Это классическая проблема из области вычислительной геометрии и кинематики, которую можно разбить на несколько логических шагов. Цель — найти "безопасную" область конфигураций (углов поворота), где нет столкновений.
Ваше описание "чтобы черные отрезки не пересекались с зелеными, а были между ними всегда" — это ключевой момент. Это можно интерпретировать как две более строгие геометрические задачи:
Параллельность: Полоса, образованная черными линиями, должна быть параллельна полосе, образованной зелеными линиями.
Вложение: Черные отрезки должны полностью находиться внутри "коридора", очерченного зелеными отрезками.
Давайте решим эту задачу по шагам.
Шаг 1: Упрощение и формализация задачи
Для начала введем обозначения:
α (альфа) — угол поворота черных отрезков вокруг точки O1.
β (бета) — угол поворота зеленых отрезков вокруг точки O2.
γ (гамма) — угол поворота всей синей пластины (вместе с O1 и черными отрезками) вокруг O3.
Иерархия вращений:
Сначала вся система {A1B1, A2B2, O1} поворачивается на угол γ вокруг O3. Это дает нам новые координаты для O1, A1, B1, A2, B2.
Затем, уже в новой системе, отрезки {A1B1, A2B2} поворачиваются на угол α вокруг (нового) O1.
Зеленые отрезки просто поворачиваются на угол β вокруг O2.
Шаг 2: Условие параллельности (самое важное упрощение)
Чтобы черные линии были "между" зелеными, они должны быть параллельны друг другу. Это самое сильное ограничение, которое сразу связывает углы α и β.
Начальные углы:
Вычисляем начальный угол наклона черных линий, θ_black_init. Это можно сделать с помощью вектора (B1 - A1). θ_black_init = atan2(B1.y - A1.y, B1.x - A1.x).
Аналогично, начальный угол зеленых линий: θ_green_init = atan2(D1.y - C1.y, D1.x - C1.x).
Конечные углы:
Итоговый угол черных линий после всех вращений будет: θ_black_final = θ_black_init + γ + α.
Итоговый угол зеленых линий: θ_green_final = θ_green_init + β.
Условие: Для параллельности θ_black_final должен быть равен θ_green_final.
θ_black_init + γ + α = θ_green_init + β
Отсюда мы получаем прямую зависимость между β и α:
β = α + γ + (θ_black_init - θ_green_init)
Это гениальное упрощение! Теперь нам не нужно перебирать пары (α, β). Для любого выбранного α (и заданного γ) мы можем однозначно вычислить β, при котором системы будут параллельны. Задача свелась к поиску подходящего α.
Шаг 3: Условие вложения (поиск диапазона для α)
Теперь, когда линии параллельны, нам нужно убедиться, что черные отрезки находятся внутри "зеленого коридора". Это условие можно разбить на два:
Поперечное вложение: Полоса, образованная черными линиями, должна быть уже и находиться внутри полосы, образованной зелеными линиями.
Продольное вложение: Проекция черных отрезков на общую ось движения должна лежать внутри проекции зеленых отрезков.
Алгоритм решения:
Для заданного угла γ:
Подготовка (выполняется один раз):
Вычислите Δθ = θ_black_init - θ_green_init. Теперь β = α + γ + Δθ.
Найдите ширину черной и зеленой полос (W_black, W_green). Это расстояние между параллельными прямыми A1B1 и A2B2, и C1D1 и C2D2 соответственно.
Определите векторы от центров вращения до "центров" полос. Например, вектор от O1 до середины отрезка, соединяющего A1 и A2.
Основной цикл (для поиска α):
Мы ищем диапазон допустимых значений α. Это можно сделать аналитически (сложно) или численно (проще и надежнее).
Численный метод (рекомендуется):
Перебираем угол α с небольшим шагом (например, от -180° до +180° с шагом в 1°). Для каждого значения α:
Вычисляем β: β = α + γ + Δθ.
Находим текущие положения всех точек:
O1_new = rotate(O1, O3, γ)
A1_init_rot = rotate(A1, O3, γ) (и так для B1, A2, B2)
A1_final = rotate(A1_init_rot, O1_new, α) (и так для B1, A2, B2)
C1_final = rotate(C1, O2, β) (и так для D1, C2, D2)
Проверяем поперечное вложение:
Найдем уравнения двух зеленых прямых в виде ax + by + c = 0. Пусть это L_C1D1 и L_C2D2. Нормализуем их так, чтобы вектор нормали (a, b) был одинаковым.
Чтобы черные точки P (A1_final, B1_final, A2_final, B2_final) были между зелеными линиями, знаки (aP.x + bP.y + c1) и (aP.x + bP.y + c2) должны быть противоположными для всех четырех точек.
Упрощенная проверка: Найдите перпендикулярное расстояние от центральной оси зеленой полосы до центральной оси черной полосы (d_centers). Условие вложения: d_centers + W_black/2 <= W_green/2.
Проверяем продольное вложение:
Возьмем одну из линий, например, A1_final B1_final, как общую ось.
Спроецируем все 8 конечных точек (A1_final...D2_final) на эту ось.
Проекции черных точек образуют на оси отрезок [min_black, max_black].
Проекции зеленых точек образуют на оси отрезок [min_green, max_green].
Условие вложения: [min_black, max_black] должен полностью содержаться внутри [min_green, max_green]. То есть, min_green <= min_black и max_black <= max_green.
Результат:
Если оба условия (поперечное и продольное) выполнены, то текущий угол α является допустимым.
Собираем все допустимые α в один или несколько диапазонов.
Псевдокод
# --- Начальные данные ---
# Координаты точек A1, B1, A2, B2, C1, D1, C2, D2
# Координаты центров вращения O1, O2, O3
# --- Подготовка ---
theta_black_init = atan2(B1.y - A1.y, B1.x - A1.x)
theta_green_init = atan2(D1.y - C1.y, D1.x - C1.x)
delta_theta = theta_black_init - theta_green_init
# --- Входные данные для симуляции ---
gamma = ... # Заданный угол поворота вокруг O3
# --- Основной расчет ---
valid_alpha_ranges = []
for alpha in range(-180, 181): # Перебор с шагом в 1 градус
# 1. Вычисляем зависимый угол beta
beta = alpha + gamma + delta_theta
# 2. Вычисляем текущие координаты всех вершин
# Для черных (сначала вокруг O3, потом вокруг O1)
O1_new = rotate(O1, O3, gamma)
A1_temp = rotate(A1, O3, gamma)
# ... и для B1, A2, B2
A1_final = rotate(A1_temp, O1_new, alpha)
# ... и для B1, A2, B2
# Для зеленых (вокруг O2)
C1_final = rotate(C1, O2, beta)
# ... и для D1, C2, D2
# 3. Проверка вложения
is_transverse_fit = check_transverse_containment(A1_final, ..., D2_final)
is_longitudinal_fit = check_longitudinal_containment(A1_final, ..., D2_final)
if is_transverse_fit and is_longitudinal_fit:
# Этот alpha подходит. Добавляем его в список/диапазон.
add_to_valid_ranges(alpha)
# В valid_alpha_ranges теперь находятся все "безопасные" углы alpha
# для заданного gamma. Для любого alpha из этого диапазона,
# соответствующий beta гарантирует бесконфликтное прохождение.
Этот алгоритм позволит вам для любого положения "синей пластины" (γ) мгновенно вычислить все возможные углы α и β, при которых механизм будет работать без столкновений. "Оптимальность" здесь заключается в том, что мы не ищем одно решение, а находим всю область допустимых решений, из которой можно выбрать любое.
нейрокал пугает... но я уже решил задачу и у меня оптимальней чем у нейрокала вышло. хотя бы потому что я не перебираю никаких углов вот тут результат >>3466762 и описание >>3466752
алсо бтв. как ты нейрокалу грамотно строишь задачу, чтобы он понял? как он в таком случае понимает где эти отрезки все проходят?
>Это классическая проблема из области вычислительной геометрии и кинематики
вот это вообще убило. я пытался гуглить и ничего похожего даже близко не мог найти, именно чтобы мой случай был рассмотрен, если это настолько "классически". от куда она эту инфу всю берет?
>алсо бтв. как ты нейрокалу грамотно строишь задачу, чтобы он понял? как он в таком случае понимает где эти отрезки все проходят?
Я ему просто показываю твои картинки + текст твоего поста прикладываю. Gemini 2.5 pro.
>я пытался гуглить и ничего похожего даже близко не мог найти, именно чтобы мой случай был рассмотрен, если это настолько "классически". от куда она эту инфу всю берет?
Короче говорит, что ты его не так понял. Он имел ввиду не конкретно твою задачу, а подзадачи которые распадаются на прямую и обратную кинематику, и на обнаружение столкновений. Посоветовал гуглить по словам "line segment intersection algorithm, separating axis theorem tutorial, robotics configuration space", а также "inverse kinematics 2D, analytical vs numerical IK, robot arm kinematics".
>но я уже решил задачу и у меня оптимальней чем у нейрокала вышло. хотя бы потому что я не перебираю никаких углов вот тут результат >>3466762 и описание >>3466752
Отличный ход мысли! Ваш способ решения гораздо элегантнее, чем перебор углов, и стремится найти аналитическое, то есть прямое, решение. Это правильный инженерный подход.
Проблема, с которой вы столкнулись ("когда начинаю далеко вращать, синяя и красные линии начинают расходиться"), очень характерна для задач с несколькими системами координат. Давайте разберем, почему это происходит и как это исправить.
Анализ вашего метода и причина проблемы
Ваш метод интуитивно понятен:
У нас есть два объекта (шток и паз/отверстие), которые нужно направить друг на друга.
Вы соединяете их центры вращения (O1 и O2) синей линией.
Вы используете эту синюю линию как общий ориентир, относительно которого вычисляете углы поворота для штока (красная линия) и паза (зеленая линия).
Вот здесь и кроется фундаментальная ошибка.
Причина проблемы: Синяя линия (вектор O2 - O1) — это не статический, глобальный ориентир. Когда вы вращаете всю систему вокруг точки O3 (изменяете угол γ), точка O1 перемещается. Следовательно, синяя линия сама меняет и свою длину, и свой угол наклона в глобальной системе координат.
Вы пытаетесь выровнять две локальные системы (шток и паз) относительно третьей системы (линия O1-O2), которая сама является "плавающей". Это работает только в одном начальном положении. Как только вы поворачиваете базу (γ ≠ 0), ваша система отсчета "ломается".
Простыми словами: Вы говорите штоку: "Повернись так, чтобы смотреть на линию, соединяющую твой pivot с pivot'ом паза". Но когда вся база поворачивается, и шток, и эта линия поворачиваются вместе, и ваш расчет угла становится неверным.
Как исправить? (Правильный аналитический подход)
Ваша интуиция вас не подвела, нужно найти правильный "целевой" вектор. Но этот вектор должен определяться истинным геометрическим условием.
Истинное геометрическое условие: Ось штока должна пройти через центр паза (или отверстия).
Давайте построим решение на этом.
Шаг 1: Определяем целевой вектор
Зафиксируем γ (угол поворота синей пластины вокруг O3).
Найдем текущее положение центра вращения штока O1_current. Это исходная точка O1, повернутая вокруг O3 на угол γ.
Найдем текущее положение центра паза Q_current. Вот здесь самое интересное. Положение Q зависит от угла поворота β вокруг O2. То есть, Q_current = O2 + rotate(Q_initial - O2, β).
Целевой вектор направления V_target — это вектор, идущий от текущего центра вращения штока к текущему центру паза:
V_target = Q_current - O1_current
Шаг 2: Определяем текущий вектор штока
Текущий вектор направления штока V_rod зависит от двух вращений: γ (поворот базы) и α (собственный поворот). Его итоговый угол в глобальной системе координат будет θ_rod_init + γ + α.
Шаг 3: Составляем уравнение
Для того чтобы шток вошел в паз, нам нужно выполнить два условия одновременно:
Параллельность: Шток должен быть параллелен пазу. Отсюда мы знаем нашу старую добрую связь: β = α + γ + const.
Соосность: Направление штока V_rod должно совпадать с направлением целевого вектора V_target.
V_rod || V_target
vector_from_angle(θ_rod_init + γ + α) || (O2 + rotate(Q_initial - O2, β)) - O1_current
Теперь подставляем β из условия параллельности в это уравнение. У нас останется одно векторное уравнение с одной неизвестной — α.
Это уравнение будет довольно громоздким (содержать синусы и косинусы от α), но его можно решить численно или, в некоторых случаях, аналитически.
Упрощенный и надежный алгоритм (комбинированный)
Вместо того чтобы решать сложное тригонометрическое уравнение, можно использовать ваш же подход, но с исправленной логикой.
Цель: Найти такой угол α, при котором линия штока пройдет через центр паза.
Задаем γ (положение синей плиты).
Вычисляем O1_current = rotate(O1, O3, γ).
Находим связь β = α + γ + (θ_rod_init - θ_slot_init). Это гарантирует параллельность.
Теперь нам нужно найти α. Для этого мы можем использовать итерационный или численный метод, который найдет корень уравнения. Но проще всего сделать следующее:
Предположим, что шток и паз уже соосны.
Тогда их общее направление должно быть задано вектором, соединяющим "эффективную точку вращения" штока и "эффективную точку вращения" паза.
"Эффективная точка вращения" паза — это его центр Q, вращающийся вокруг O2.
"Эффективная точка вращения" штока — это точка на его оси, которая вращается вокруг O1. Для простоты, пусть это будет сам O1.
Алгоритм для прямого вычисления:
Для заданного γ вычисляем O1_current = rotate(O1, O3, γ). O2 остается на месте.
Определяем целевое направление. Это направление вектора от O1_current к O2. ВНИМАНИЕ: это приближение, которое будет работать, только если шток и паз проходят прямо через свои центры вращения. Если они смещены, то нужно использовать смещенные точки.
V_target_dir = normalize(O2 - O1_current)
Вычисляем требуемый итоговый угол штока.
θ_final_rod = atan2(V_target_dir.y, V_target_dir.x)
Находим угол поворота α.
Мы знаем, что θ_final_rod = θ_rod_init + γ + α.
Отсюда: α = θ_final_rod - θ_rod_init - γ.
Находим угол поворота β.
θ_final_slot должен быть равен θ_final_rod.
θ_final_slot = θ_slot_init + β.
Отсюда: β = θ_final_rod - θ_slot_init.
Этот алгоритм намного проще и должен работать, но его точность зависит от того, насколько корректно O1 и O2 представляют "оси действия" ваших механизмов. Если шток или паз сильно смещены относительно центров вращения, этот метод даст погрешность.
Резюме:
Ваша идея верна, но вы выбрали неправильный "якорь" для системы отсчета. Вместо того чтобы привязываться к плавающей линии O1-O2, нужно решать задачу исходя из фундаментального физического требования: ось штока должна пройти через центр паза. Мой последний предложенный алгоритм — это прямое вычисление углов на основе этого требования в его упрощенной форме.
а что за нейронка конкретно? чатгпт дает какие-то другие ответы
Конкретно я уже назвал имя - Gemini 2.5 pro 06-05 preview от гугла https://aistudio.google.com/gallery чатгпт говно, у него слабее аналитические способности.